zuloolion.blogg.se

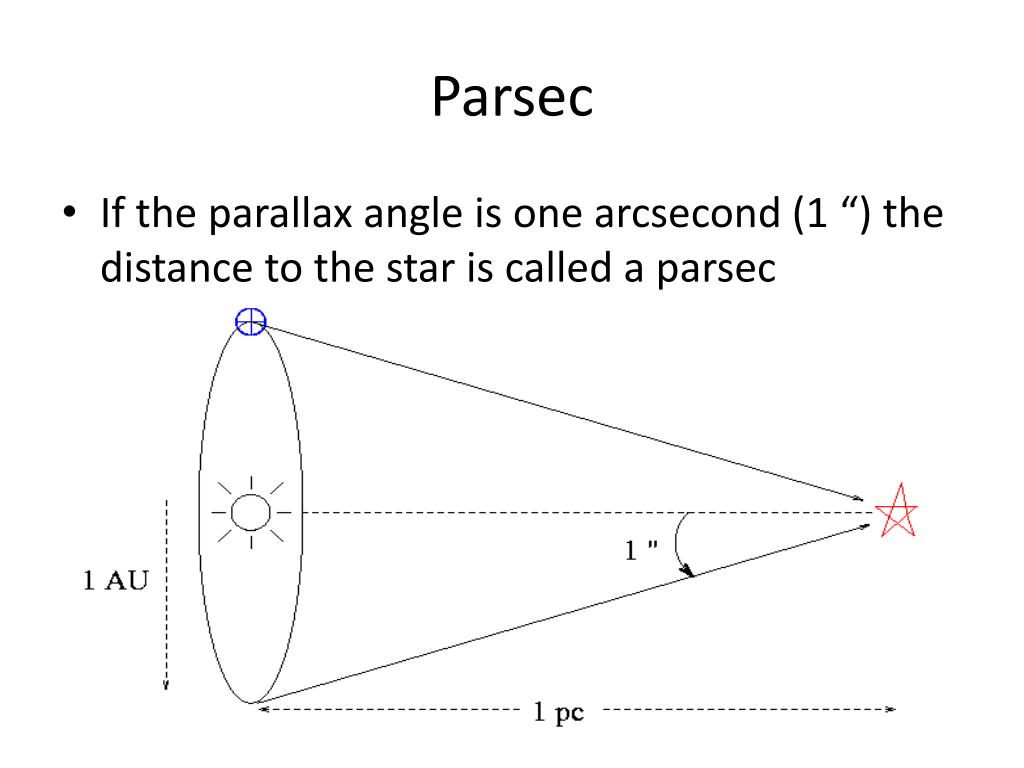
When the planet is under the horizon the planet cannot be observed at P. The ability to measure distances in space is particularly useful. Astronomers can use data from parallax measurements to calculate the parsec, which is the world’s largest unit of distance. When the planet is at the horizon the diurnal parallax is maximum. The distance to the star is indicated by D and is expressed in parsecs (1 parsec 3.26 lyr) The baseline distance between the Sun and the point of. The parallax effect is used in astronomy to calculate parsecs. Note that the diurnal parallax is zero when the planet is in the zenith (above the observer at P) both α and α 0 are zero. When p is measured in seconds of arc and the distance d in parsecs, the simple relation d 1/ p holds. Similarly, the angle α 0 is the geocentric zenith distance (measured from C, the center of the Earth). By definition of the parsec, a star at 1pc has a parallax of 1.0, meaning that its distance is 206,264 au, corresponding also to 3.26 light-years or 3.1 × 10. Annual parallax is normally measured by observing the. The angle can be determined, for instance, against the background of fixed stars. The parsec (3.26 light-years) is defined as the distance for which the annual parallax is 1 arcsecond. The observer observes a planet (or another object in our solar system) under an angle α with the zenith, this angle is the topocentric zenith distance of the planet.

Perpendicular to the plane is the zenith. 2, an observer at P sees the surface of the Earth as a plane bounded by the horizon.

In astronomy, the diurnal parallax is the parallax caused by the diurnal (daily) rotation of the Earth. The distance p 2−p 1 is the (linear) parallax. An observer at viewpoint 1 measures the object to be at p 1 on the scale and an observer at viewpoint 2 measures it at p 2. For comparison, the resolution of the Hubble Space Telescope is #.05 " arc-seconds"#, so even Hubble would not be able to detect the necessary angular shift of the nearest galaxy to effectively use parallax as a measure of its distance.Fig. Stellar parallax is just one of the ways in which astronomers can measure the distance to stars. The true distance to the star can be calculated from its parallax using basic trigonometry. An arcsecond is a unit for small angles, such as the parallax one. The parallax of a star is defined as the difference in apparent position of the star when observed from the Earth on opposite sides of the Sun’s orbit. Some important points about the previous relationship: The distance to stars is usually a huge number, so the parallax angle is really tiny. Using the slightly modified parallax formula, we can find the necessary parallax angle to measure the distance to Andromeda. D 1/P, where: D Distance between the star and the Earth, in parsecs ( pcs) units and P Parallax angle, in arcseconds ( arcsec) units. , 'It's the distance that an object needs to be from EARTH in order for it to have a parallax angle of one arc second. The distance to M31 has been measured using other techniques to be #2.5 *10^6" light years"#, or #7.6*10^5 " parsecs"#. The Andromeda Galaxy, M31, is the nearest major galaxy to the Milky Way. #1" parsec"# is equal to about #3.3 " light years"#. The distance is measured in parsecs, and the parallax angle is in arc-seconds.

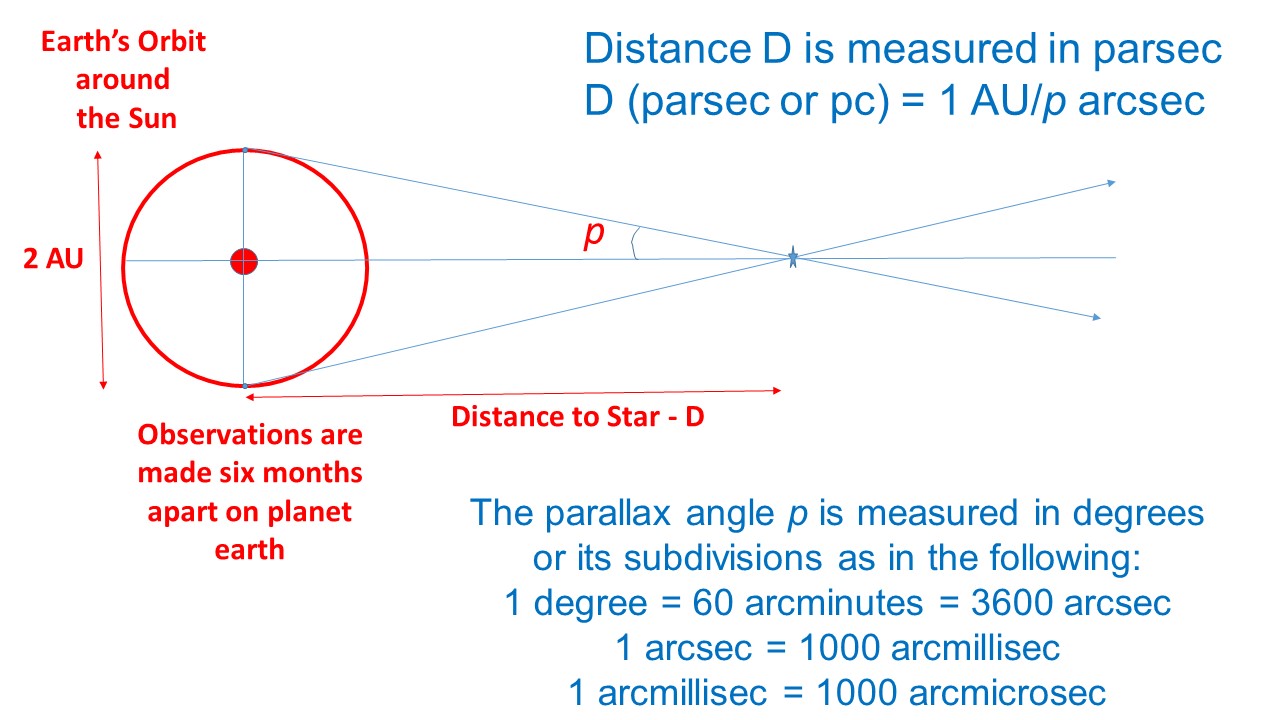
Q: How many meters are in one parsec How many. The parallax formula gives the distance, #d# to an object given the parallax angle, #p#. The Parsec Star, Parallax ( of arc), Distance (l.y) a Centauri, 0.750, 4.3 Barnards star, 0.545, 6.0 Sirius, 0.377, 8.6 Procyon, 0.285, 11.4. A parsec is defined as the distance at which a star will have a heliocentric parallax half-angle of 1 arcsecond. The parallax formula gives the distance, Math Processing Error to an object given the parallax angle, Math Processing Error. Astronomers make observations from Earth on either side of the sun. By definition, parsec (pc) is the distance from the Sun to a star that has a parallax of 1 (1 arc second) Parallax Formula: Distance (in pc) 1/parallax (in arcsec) One parsec 206,265 AU or 3.3 light-years As the distance increases to a star, the parallax decreases. Astronomers make observations from Earth on either side of the sun. Explanation: Parallax works by measuring the apparent shift of an object against its background from two different vantage points. Parallax works by measuring the apparent shift of an object against its background from two different vantage points.